وحدة قياس الزاويا
وحدة قياس الزاويا
دليل
- 1 وحدات قياس الزوايا
- 1.1 درجة
- 1.2 راديان
- 2 زاوية الانتقال
- 3 مثال على تحويل وحدة الزاوية
- 4 المراجع
وحدة الزاوية
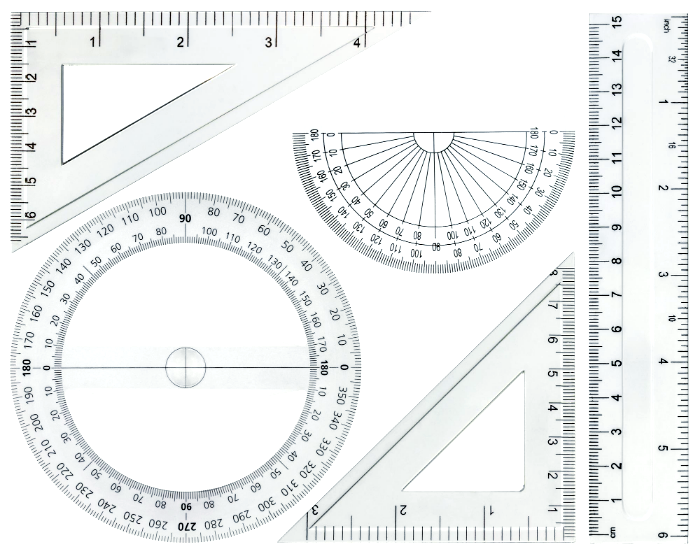
تنقسم الوحدات المستخدمة لقياس الزوايا إلى الأنواع التالية:
الدرجة
وحدة الدرجة (الإنجليزية: DEGREE) هي الأكثر استخدامًا من بين جميع وحدات القياس الأخرى. درجة الدورة هي 360 درجة ، كل دورة مقسمة إلى 60 دقيقة ، وكل دقيقة مقسمة إلى 60 ثانية. الدرجة الرمز عبارة عن دائرة صغيرة تصنف الزوايا حسب قياسها بالدرجات على النحو التالي:
- الزاوية الحادة: زاوية أكبر من 0 درجة وأقل من 90 درجة.
- الزوايا الدائرية: زاوية تساوي 90 درجة.
- زاوية الفتح: زاوية أكبر من 90 درجة وأقل من 180 درجة.
- الزاوية اليمنى: زاوية 180 درجة.
راديان
يتم تمثيل وحدة الراديان بنصف قطر الدائرة ، 1 راديان يمثل قياس الزاوية المركزية لطول قوس يتم قطعه على طول نصف قطر الدائرة ، ويتم تمثيل هذه الوحدة بالرمز (RAD) ، وهي فترة واحدة من هذه الوحدات هي 2Π.
زاوية التحويل
يمكن إجراء التحويل بين الراديان والدرجات بسهولة وفقًا للصيغة التالية:
زاوية الراديان = الدرجات × 180 / Π
درجات الزاوية = زاوية راديان x Π / 180
يوضح الجدول أدناه بعض الزوايا المشتركة للوحدتين:
|
درجات الزوايا
|
Radian Angle
|
| 360 |
2Π
180 Π 90 Π / 2 60 Π / 3 45 Π / 4
مثال على تحويل وحدة الزاوية
يمكن توضيح التحويل بين وحدات الزوايا من خلال المثال التالي:
المثال الأول:.
درجة الزاوية الحادة 30 درجة ، كيف يتم التعبير عنها بالراديان؟
الحل:
-
- زاوية الراديان = درجة × 180 / π
يتم ضرب قيمة
-
- 30 في (π / 180).
يعطي
- π / 6 ، لذا فإن 30 درجة تساوي π / 6 راديان.
المثال الثاني:
إذا كان قياس الزاوية المنفرجة 120 درجة ، فعبّر عن هذا المقدار بوحدات الراديان.
الحل:
- زاوية الراديان = درجة × 180 / π
- يتم ضرب قيمة 120 في (π / 180).
- النتيجة هي 2π / 3 ، لذا فإن 120 درجة تساوي 2π / 3 راديان.
المثال الثالث :.
إذا كان قياس الزاوية 7π / 6 راديان ، فكيف يتم التعبير عنها بالدرجات؟
الحل:
-
- الزاوية بالدرجات = الزاوية بالتقدير الدائري × Π / 180
- ضرب القيمة 7Π / 6 في (180 / Π).
يعطي
- 210 درجة ، لذا فإن 7π / 6 راديان يساوي 210 درجات.
المثال الرابع:.
إذا كان قياس الزاوية الحادة π / 8 راديان ، فعبِّر عن هذه الكمية بالدرجات.
الحل:
-
- الزاوية بالدرجات = الزاوية بالتقدير الدائري × Π / 180
- π / 8 مرات 180 / π.
يعطي
- 22.5 ، لذا π / 8 راديان يساوي 22.5 درجة.
المثال الخامس :.
إذا كان قياس الزاوية 4Π / 5 ، فحدد نوع الزاوية المراد تحويلها إلى درجات.
الحل:
- الزاوية بالدرجات = الزاوية بالتقدير الدائري × Π / 180
- 4π / 5 مرات (180 / π).
- النتيجة هي 144 ، لذا 4π / 5 راديان يساوي 144 درجة.
- تعتبر الزاوية التي مقدارها 144 درجة منفرجة لأنها تقع بين 90 و 180 درجة.
المثال السادس :.
إذا كان قياس الزاوية π / 12 ، فحدد نوع الزاوية المراد تحويلها إلى درجات.
الحل:
- الزاوية بالدرجات = الزاوية بالتقدير الدائري × Π / 180
- ضرب القيمة π / 12 في (180 / π).
- يساوي 15 ، لذا π / 12 راديان يساوي 15 درجة.
- تعتبر الزاوية 15 درجة حادة لأنها أقل من 90 درجة.
المراجع
- ^ ، Spark Notes ، تم استرجاعه في 23 ديسمبر 2021. تم تحريره.
- ^ ، موسوعة ، تم الوصول إليه في 29 مايو 2018 ، 23 ديسمبر 2021. تم تحريره.
- ، BYJUS ، تم استرجاعه في 23 ديسمبر 2021. تم تحريره.
- ، EXPII ، تم استرداده في 23 ديسمبر 2021. تم تحريره.
- ، CUEMATH ، تم استرداده في 13 أبريل 2022. تم تحريره.
- ، PURPLEMATH ، تم استرداده في 13 أبريل 2022. تم تحريره.